Here are the values of the density function stored as three dimensional, discrete grid, a big array. A possible source is for example the editor Acropora by Voxelogic. It can export it’s data as 3D DDS texture where each pixel can be interpreted as 32 bit float value. Naturally, the volume component supports it’s own optimized saving and loading of discrete grids, a later article covers this.
All in all, this article is quite math heavy, but every formula is simple on its own and can be literally translated into code, so don’t be scared.
Beside the density, it’s important to know what world dimensions the exported volume has. With all those data are the density and the gradient of a specific coordinate calculated. As preparation, the coordinate is transformed from worldspace into the space of the grid with
as the dimension of the grid and
as the dimension of the volume.:
To give some options to the user to decide between loading time and quality, two methods to calculate the density and four for the gradient are given.
Calculating the density value can be done by interpolating via a “Nearest Neighbor” interpolation or a trilinear interpolation.
The nearest neighbor interpolates by simply choosing the grid coordinate which is closest to [Tö05, P. 112 – 113]:
is a function to get the value of the 3D grid at the integer coordinate (x, y, z). So the wanted density value is given by
.
Although the nearest neighbor interpolation is very fast, a higher quality can be achieved by using the trilinear interpolation [Bou99]:
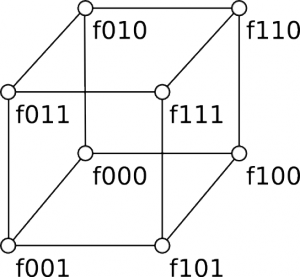
The range of x, y and z is from 0 to 1 with (0, 0, 0) being the vertex and (1, 1, 1) being the vertex
in figure 1. So the given coordinate must be normalized into this range and translated into the origin of the grid space. In case of the discrete grid, only the translation is needed because the array values already have a distance of one to each other.
is the grid value
. Respective is
the grid value
.
The gradient can be calculated either by using the nearest neighbor interpolation by evaluating or by trilinear interpolation.
to
are in this case the gradients at the cubus vertices instead of the grid values.
is the calculation of the gradient at an integer coordinate. It can be calculated either like Lorensen and Cline in the original Marching Cubes paper [LC87, P. 3] or with a Sobel filter.
This is the Marching Cubes version:
The division by the cube length of the original version is left out here, because its 1 anyway in the grid.
A second possibility is the determination with a Sobel filter which adds a low pass filter and so is less prone to noise in the grid [Tö05, P. 176 – 178].
with
and
and
Experience has shown, that the configuration with using trilinear interpolation for the density and nearest neighbor for the gradient without Sobel filter gives good results while keeping the loading time reasonable.